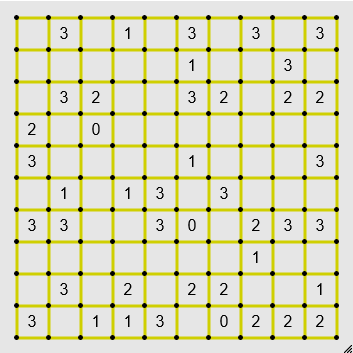
Slitherlink (or "Loopy")
Nikoli
Online Version (Other Online Versions: 1)
In Slitherlink, you have a grid with numbers in each square, and dots as the corner of each square. Your goal is to place edges, each connecting two dots, to create a looping path. No loose ends, no branching or self-intersecting paths. The numbers represent how many edges of the square are filled in.
Here are a few simple ones.
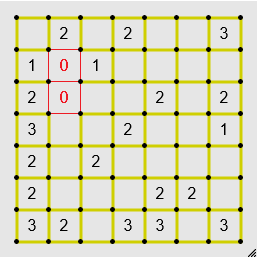
The solve usually always begins with removing possible edges near zeroes.
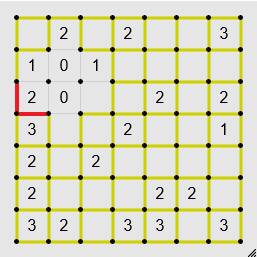
If a square with number n has exactly n possible edges around it, they're all edges.
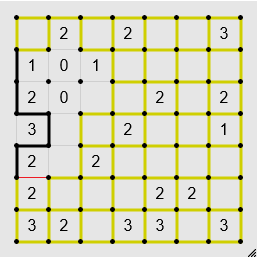
If a square with number n has exactly n filled edges around it, no other possible edge is an edge.
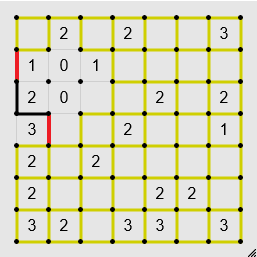
If a dot with one definite edge has exactly one other possible edge, the possible edge is an edge.
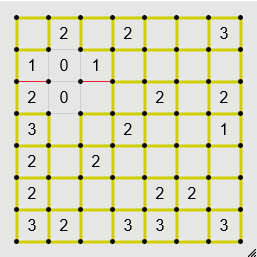
If there's no way for a possible edge to continue, it's not an edge.
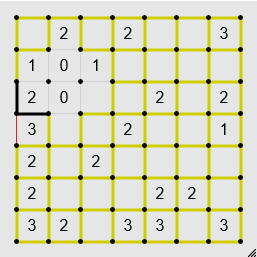
If a possible edge connects with a dot that already has two edges, it's not an edge.
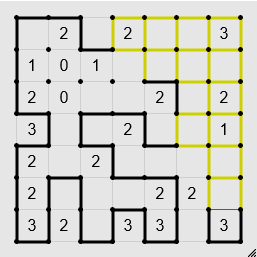
If a possible edge would complete a path too small, and not including all of the numbers, then it's not an edge.
These can sometimes solve puzzles on their own, but to solve most puzzles, you'll need these slightly more advanced strategies:
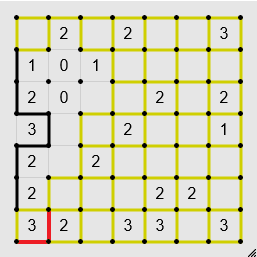
If an edge leads to a square with a 3 inside it, you can fill in the two edges that aren't connected to the edge. This one along with the previous ones are usually enough.
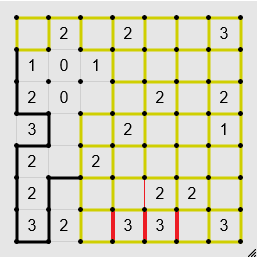
If there are a line of threes, you can fill in the edges in between each of them, as well as the ends, and clear the edges above the edges in between each of them.
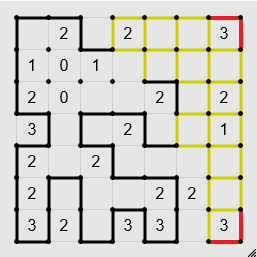
If there's a three in a corner (i.e. only two possible edges in a dot), you can fill the edges of the corner.